





|
【連載 統計解析力アップ講座】 演習;統計的品質管理(1)
|
データ解析の基礎ともいえる統計的品質管理についての講座です。例題を通して統計解析についての基礎力アップを目指します。今回は初回として、統計的な考え方とはどんなことなのかをわかりやすく説明します。 ○例題1 工程の製造条件を変更したところ、次のように収量が平均で5%アップしました。 この状態のまま製造を継続してもよいでしょうか?
●答 データの特性というのは平均だけではありません。もうひとつ重要な特性があります。 それがデータ(母集団)の広がりを表すばらつきです。 ばらつきを簡単に示すにはデータの最大値と最小値の差=範囲を求めます。
変更前は範囲9の間に収まっていたデータが、変更後には43もの範囲に広がっています。 収量の安定性が悪くなっていますので、安定性の向上を図らなければなりません。 一般にデータのばらつきは、データが正規分布という分布に従うと仮定して‘標準偏差’という数値で示されます。 標準偏差が大きいほどデータのばらつきが大きいことを示します。
○例題2 次のデータについて、ばらつきを含めたデータの状態を詳しく調べてください。
●答 まずデータの状態をグラフ化します。この場合、データの分布状態を直感的に理解しやすいヒストグラムというグラフを描きます。横軸に範囲を区切り、縦軸にその区切りごとに現れたデータの数(頻度)を表したグラフがヒストグラムです。Excelを用いると次のようなヒストグラムを簡単に描くことができます。 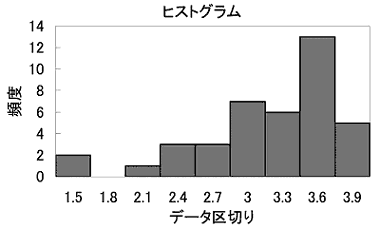
データの分布の状態を数値で表現するのが「基本統計量」です。ヒストグラムで表されるようなデータの分布を数値で表現します。基本統計量はExcelの分析ツールを利用すると次のように求められます。 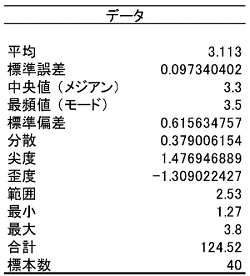
○基本統計量基本統計量のそれぞれの数値には次のような意味があります。1) 平均 データの分布の中心を表す数値として最もよく利用される数値です。全データを加え合わせた値をデータの数で割って求められる「相加平均(単純平均、算術平均とも)」が使用されます。平均にはこれ以外に全データ(データ数n)を掛け合わせてn乗根をとる「相乗平均(幾何平均とも)」、データ分の1(データの逆数)の総和でデータ数を割る「調和平均」があります。データの分布を見る場合の平均には相加平均を使います。 データをとしたとき、それぞれの平均を求める式は次のようになります。あわせて今回のデータから求めたそれぞれの平均も次に示します。
この3つの平均には、相加平均≧相乗平均≧調和平均、という関係が必ず成立します。相乗平均は連続した増加率の平均を求める場合などに使用します。利率が変動する場合の複利計算で、平均成長率を計算することができます。調和平均は走行速度の平均をとる場合などに使用します。 2) 最小、最大、範囲 データの中で最小の値と最大の値、およびその差を示す数値です。範囲の大きさにはデータのばらつきの大きさが強く現れ、標準偏差の代わりにばらつきの大きさを簡易的に示す数値として利用されます。 3) 中央値(メジアン)、最頻値(モード) どちらも平均と同様、データの分布の中心を示す数値です。中央値(メジアン)はその数値より上のデータ数と下のデータ数が等しい、つまりデータ数を二分する値を指します。今回のデータでは3.30が中央値です。 最頻値(モード)は最も高頻度で出現したデータの値を示します。今回のデータでは最頻値は3.50です。データを見ると確かに3.50という値がもっとも多く8回現れています。 先ほど求めたヒストグラム上に平均、中央値、最頻値を示してみます(データ区切りの値が各棒の右端の値であることにご注意ください)。平均、中央値、最頻値の順で値が大きくなっていることがよくわかります。 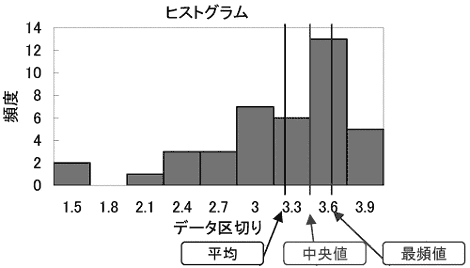
このヒストグラムに示されるデータの分布の状態を曲線で近似すると、次のような形となります。 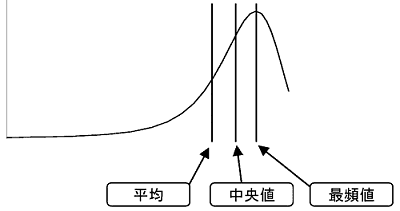
もしこの形が次のような左右対称になる形だったら、どうでしょう。 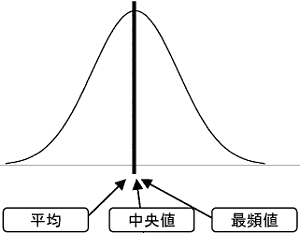
平均、中央値、最頻値がぴったり重なってしまいます。この3つの値を区別する必要がなくなり、どれか1つで間に合うことになります。このような形のデータの分布、これが非常に重要な分布で、多くの現実のデータがこの形に分布します。実は‘偶然によって支配されるデータ’は、必ずこの形の分布になります。 簡単に、サイコロを2つ振る場合を考えてみます。2つのサイコロの目は偶然だけによって決定されるとすると、その目の出現は組合せの数に従います。 つまり、次のような分布で現れることになります。 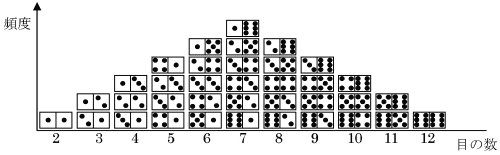
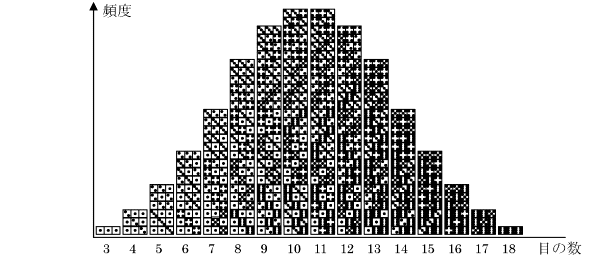 このように、偶然の現象はこの形に分布することが必然といえるのです。この分布を「正規分布」と呼びます。データを‘統計的に扱う’というのは、データの分布が正規分布になっているとすることが基本となります。 もし、測定したデータの分布が正規分布になっていないとき、それは偶然以外のなんらかの理由が必ず存在していると判断することができるのです。 4) 標準偏差、分散 標準偏差、分散ともデータの分布の広さ(ばらつきの大きさ)を示す数値です。データが平均に対してどれぐらい離れたところまで広がっているかを示すには、まず各データと平均の差を求めればよいのですが、ただ平均との差を取るだけではデータによって符号が+、−と変わり、すべての差を合計すると0になってしまいます。 そこで符号を+に合わせるため、すべてのデータの平均との差を2乗します。この2乗した値を元にして求めた数値が「分散」で、分散の平方根をとってデータとの関連をわかりやすくした数値が「標準偏差」です。 データを、平均をμとすると、分散、標準偏差は次のような式で計算できます。右側に今回のデータでの計算結果もそれぞれ示します。
標準偏差が0.6156であることをヒストグラム上で示すと次のようになります。 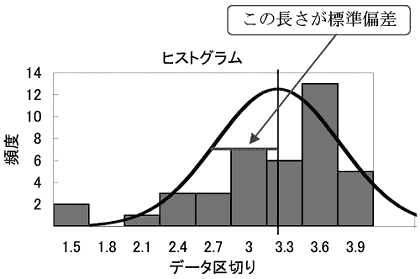
このように、標準偏差を図示すると自動的に正規分布の曲線が引けます。正規分布は平均と標準偏差で定義できるからです。つまり、標準偏差を考えることとデータの分布が図のように正規分布であると考えることは同じことだといえるのです。 5) 尖り度、歪み度(とがり度、ゆがみ度) 尖り度、歪み度はデータの分布が正規分布からどれだけ離れているかを示す数値です。尖り度、歪み度ともデータが正規分布ならその値は0になります。 平均から外れすぎたデータによって分布の裾野が広くなると尖り度の値が大きくなります。逆に正規分布よりデータが中心にかたまっていると尖り度は負の値となります。 データの分布が左右対称でなく値の小さい方(左側)に偏ると歪み度が大きくなり、大きい方(右側)に偏ると歪み度は負の値となります。 データを、平均をμ、標準偏差をσとすると、尖り度、歪み度は次の式で求められます。また、合わせて今回のデータから求めた値も示しておきます。
今回のデータでは、尖り度は0より大きな値となり、平均から外れた値によって正規分布より裾野が広い形になっていることを示しています。また、歪み度は負の値ですので分布が右側に偏っていることを示します。 参考までに、正規分布は次のような数式で表現されます。 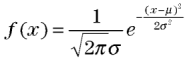
正規分布は数式で表現されるので、データの状態を数学的に表現、解析するのに非常に便利です。また、パラメータが2つしかありませんので、簡単にデータの状態を表現することができます。そのパラメータとは平均μ(ミュー)と、ばらつきの大きさを示す標準偏差σ(シグマ)です。あるデータの状態を、平均と標準偏差の2つの数字だけで表現することができるのです。 横軸にデータの数値、縦軸にその発生する確率(正式には度数関数といいます)をとって正規分布をグラフで表すと、次のようになります。 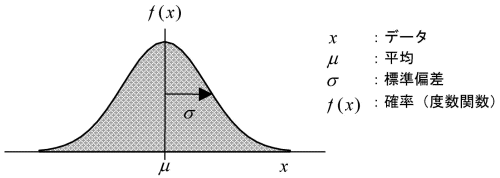
このとき、グラフで囲まれた部分が確率の全体を示します。確率全体とは100%、つまり1ですので、このグラフ全体で囲まれた面積が1になるということです。したがって、x軸上のある範囲の数値が発生する確率を知りたいときは、対応する面積を計算することで確率を求めることができます。 次の図のように、ある正規分布に対してその平均を中心に正および負の方向へ標準偏差分だけ広がった範囲「±1σ」を考えた場合、正規分布の平均μおよび標準偏差σがどのような値であっても、この範囲の面積は常に一定の値(0.683)になります。つまり、データがこの「±1σ」の範囲に入る確率は常に同じ確率(68.3%)になるのです。正規分布上で確率を考える場合、標準偏差が範囲を示す基準となります。 同様に、平均をはさんで「±3σ」の領域の面積は 0.997です。品質管理の場で、いわゆる「3シグマ」を重要視するのは、この範囲を考慮しておけば、これを外れる確率がわずか0.3%程度となるので十分実用にたる品質精度といえるからなのです。 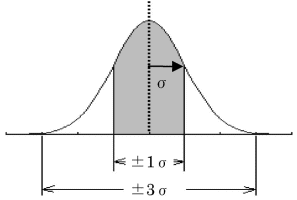
このように、標準偏差が正規分布の領域の尺度となり、その尺度に対する発生確率が一定となることが正規分布の大きな特徴です。 ○統計的品質管理とは
このように、データの広がりを正規分布の状態であるとして把握することを統計的に見るといいます。そしてデータを統計的に見た結果から集団として判断される品質を統計的品質といいます。さらに、その集団の品質が安定した状態で常に良い品質が得られるように変更や改善を行う活動を統計的品質管理と呼びます。統計的品質管理の目的は、ばらつきを抑えて品質を安定させることです。そのために、ばらつきを発生させている原因を見つけ出し、その原因についての対策や改善を実施します。ところが、データをばらつかせる原因は無数にあります。そのすべてを見つけるには多大な労力がかかりますし、それは不可能かもしれません。どうすれば良いのでしょう? 実は、無数の原因の中には品質に大きな影響を与えているものもありますが、適切に管理が行われているからとか、もともとその変動が品質に影響しない性質のため、現実の品質変動にほとんど影響をおよぼさないものがあります。 一般に品質に影響を与える原因と影響の度合いをグラフに示すと、次のように「数は少ないが影響が大きいもの(原因1、2)」と「数は多いが影響は小さいもの(原因3〜6)」に2分されます。 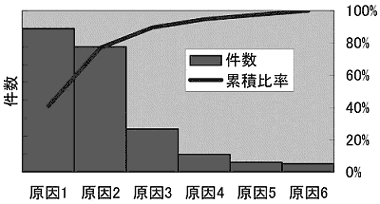
この図はパレート図と呼ばれるもので、もともと、イタリアの経済学者パレートによって、国民所得の大部分が一部の高所得者により獲得されていることを示すのに使用されました。 この法則はこれ以外の「無数の原因によって影響される事象」によくあてはまることが知られ、品質管理においてもパレートの法則として適用されます。 JIS Z8101-2(統計的品質管理用語)では「項目別に層別して、出現頻度順に並べるとともに、累積和を示した図。例えば不適合品を不適合の内容の別に分類し、不適合品数の順に並べてパレート図を作ると不適合の重点順位がわかる。」と明記されています。経験的に、影響の大きい2割の原因で全件数の80%を占めるので「2割80%の法則」と言われます。「1割60%」と言われることもあります。 この原因1、2のような、ばらつきに大きく影響する原因を抽出して対策することで、影響の小さい原因による小さな誤差だけで品質が変動する「品質が安定した状態」にすることができます。これが統計的品質管理の目的です。統計的品質管理では影響の大きい原因を異常原因、影響の小さい原因を誤差原因と呼んで区別します。隠れている異常原因を抽出し、対策・改善することが統計的品質管理の目的なのです。 第1回目、お疲れ様でした。第2回では検定の考え方についてわかりやすく説明します。 <参考文献> ・「Excelでできる統計的品質管理」(同友館) ・「Excelでできるデータ解析入門―すぐに応用できる13事例」(同友館) ・「Excelで学ぶ営業・企画・マーケティングのための実験計画法」(オーム社)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


